Unlocking the efficiency with algorithms

⚡️ TL;DR
In this post, we explore how the choice of algorithms can significantly impact the efficiency of your programs. We’ll discuss the importance of selecting the right algorithm and provide examples, such as sorting algorithms, to illustrate the differences in performance.

Some posts ago, we talked about the importance of data structures. Now, we are going to discover that even if we decide on a particular data structure, another major factor that affects the efficiency of a program is the algorithm to use.

Although the word algorithm is often associated with computer science, it is not exclusive to it. An algorithm is a set of instructions that describe how to perform a task. For example, a recipe is an algorithm that describes how to cook a dish. In computer science, an algorithm is a set of instructions that describe how to solve a problem.

Sometimes, we’ll encounter several algorithms that solve the same problem. In today’s post, we’ll discuss how one algorithm can be faster than other by orders of magnitude. To explore this, we’ll use the example of sorting algorithms and introduce the concept of ordered arrays.

Ordered arrays

An ordered array is almost identical to the classic array, but with one key difference: the elements are sorted in ascending order. That is, every time a value is added, it gets placed in the correct position so that the values in the array are always sorted.

For example, if we have an array with the following values: [1, 3, 5, 7, 9], and we want to add the value 4. If this array were a classic array, we could inser the 4 at the end of the array, and the computer can do this in a single step. However, if the array is ordered, we’d have no coice but to insert the 4 in the correct position, which would require shifting the 5, 7, and 9 one position to the right.

Now, this is easier said than done. The computer cannot simply drop the 4 into the right slot in a sicle stepbecause it fist has to find the right place, and the shift the other values to make room for it. This is where the algorithm comes in and let’s break down the process step by step.

Let’s start with our originial ordered array: [1, 3, 5, 7, 9]. We want to add the value 4. The algorithm to insert the value 4 in the correct position would be as follows:

1. We check the value at index 0 (1) and compare it to the value we want to insert (4). Since 1 < 4, we move to its left or to its right. Because 4 is greater than 1, we know that the 4 will be inserted somewhere to the right of 1. However, we don’t know yet exactly which cell it should be inserted into. So we need to check the next cell.
2. We inspect the value at the next index (3) and since 4 is greater than 3, we move to the right again.
3. We inspect the value at the next index (5) whici is greater than the 4 we wish to insert. Since we’ve reached the first value that is greater than the value we want to insert, we can conclude tha the 4 must be place immediately to the left of this 5 to maintain the order. To do this, we need to shift data to make room for the 4.
4. We shift the 5, 7, and 9 one position to the right to make room for the 4.

[1, 3, 5, 7, 9] -> [1, 3, 5, 7, , 9] -> [1, 3, 5, , 7, 9] -> [1, 3, , 5, 7, 9] -> [1, 3, 4, 5, 7, 9] -> Done!

It seems that when inserting into an ordered array, we need to always perform a search before the actual insertion to determine the correct spot. This is one difference in performance between ordered and classic arrays. In a classic array, we can insert a value in a single step, but in an ordered array, we need to perform a search before the insertion.

We can see in the exaple that there were initially 5 elements in the array, and that insertion took 7 steps. In terms of N, we can say that for N elementes in an ordered array, the insertion took N+2 steps. Interestingly, the number of steps for insertion is the same no matter where in the ordered array we insert the value. If our value ends up toward the beginning of the ordered array, we have fewer comparisons and more shifts. If it ends up toward the end, we have more comparisons and fewer shifts. But the total number of steps is always N+2. The fewest steps we can take is N+1 and occurs when we insert the value at the end of the array since we take N steps to compare and 1 step to insert. The most steps we can take is N+2 and occurs when we insert the value at the beginning of the array since we take N+1 steps to compare and 1 step to insert.

Searching in an ordered array

Searching for a particulas valuera in a classic array means we have to check each cell one at a time until we find the value we’re looking for. This is called a linear search.

Say that we have a regular array of [15,3,7,9,2,5,8,6] and we want to find the value 22 which doesn’t exist in the array. We would have to check each value in the array one by one until we reach the end of the array and conclude that the value is not present. With an ordered array, we can stop searching as soon as we find a value that is greater than the value we’re looking for. This is because the values are sorted in ascending order, so if we find a value that is greater than the one we’re looking for, we know that the value we’re looking for is not in the array.

Here is an implementation of a binary search algorithm in Go:

   func LinearSearch(arr []int, target int) int {
     // Iterate over each value in the array
     for i, val := range arr {
       // If the value is equal to the target, return the index
       if val == target {
         return i
       }
     }
     // If the target value is not found, return -1
    return -1
  }

In this light, linear search can take fewer steps in an ordered array than in a classic array in certain situations. That said, if we are searching for a value that is at the end of the array, we would have to check every value in the array before we find it. In this case, the number of steps would be the same as in a classic array.

We have been assuming until now that the only way to search for a value in an array is to check each value one by one. However, this is not the only way to search for a value in an array. There is another way to search for a value in an array called binary search which is much faster than linear search.

Binary search

Let’s think about a child game where the child has to guess a number between 1 and 100. The child can ask the parent if the number is higher or lower than a certain value. The parent will respond with “higher” or “lower” until the child guesses the correct number. This is in a nutshell how binary search works.

Say we have an ordered array containing nine elements but the computer doesn’t know the values in the array, so we will portray the array as [ , , , , , , , , ]. We want to find the value 7. The binary search algorithm works as follows:

1. We check the value in the middle of the array. We can calculate its index by taking the array’s length and dividinf it by two. We check the value at this cell: [, , , , 9, , , , ]. The value is 9, which is greater than 7, so we know that the value we’re looking for is to the left of 9.

2. We check the value in the middle of the left half of the array: [, , 3, , 9, , , , ]. The value is 3, which is less than 7, so we know that the value we’re looking for is to the right of 3.

3. We check the value in the middle of the right half of the array: [, , 3, 5, 9, , , , ]. The value is 7, which is the value we’re looking for.

We found the value 7 in three steps. This is much faster than linear search, which would have taken four steps to find the value. The binary search algorithm is much faster than linear search because it eliminates half of the array each time it checks a value. This is why binary search is called binary search: it divides the array in half each time it checks a value.

That’s one of the advantages of ordered arrays: we have the option of binary search.

   func BinarySearch(arr []int, target int) int {
     // We define lower and upper bounds to start the search
     lower_bound := 0
     upper_bound := len(arr) - 1
 
     // We will inspect the array until the lower bound is less than or equal to the upper bound
     for lower_bound <= upper_bound {
 
       // We calculate the middle index of the array. The result is truncated to an integer
      mid := (lower_bound + upper_bound) / 2

      // If the middle element is equal to the target, we return the index
      if arr[mid] == target {
        return mid
      } else if arr[mid] < target {
        // If the middle element is less than the target, we update the lower bound
        lower_bound = mid + 1
      } else {
        // If the middle element is greater than the target, we update the upper bound
        upper_bound = mid - 1
      }
    }

    // If the target is not found, we return -1
    return -1
  }

Binary search vs linear search

With ordered arrays of small sizes, binary search is not necessarily faster than linear search. This is because binary search has a higher overhead than linear search. Let’s break it down with an example of load test with 50 elements to find the same value using both algorithms.

   const (
     size = 50
     seed = 33
   )
 
   func generateSortedArray(size int) []int {
     arr := make([]int, size)
     for i := 0; i < size; i++ {
       arr[i] = i
    }
    return arr
  }

  func generateUnorderedArray(size int) []int {
    arr := make([]int, size)
    for i := 0; i < size; i++ {
      arr[i] = rand.Intn(size)
    }
    return arr
  }

  func BenchmarkLinearSearchSorted(b *testing.B) {

    arr := generateSortedArray(size)

    b.ResetTimer()

    for i := 0; i < b.N; i++ {
      algorithms.LinearSearch(arr, size-1)
    }
  }

  func BenchmarkLinearSearchUnordered(b *testing.B) {

    arr := generateUnorderedArray(size)

    b.ResetTimer()

    for i := 0; i < b.N; i++ {
      algorithms.LinearSearch(arr, size-1)
    }
  }

  func BenchmarkBinarySearchSorted(b *testing.B) {

    arr := generateSortedArray(size)

    b.ResetTimer()

    for i := 0; i < b.N; i++ {
      algorithms.BinarySearch(arr, size-1)
    }
  }

With this test, we can see that linear search is faster than binary search when the array is small. Let’s see the results of the test:

   manu@msi:~/Projects/dsa-sample$ make test-load 
   goos: linux
   goarch: amd64
   pkg: github.com/manulorente/dsa-sample/tests/load
   cpu: AMD Ryzen 7 5825U with Radeon Graphics         
   BenchmarkLinearSearchSorted-16          39052846                26.47 ns/op
   BenchmarkLinearSearchUnordered-16       163234096               10.75 ns/op
   BenchmarkBinarySearchSorted-16          140187739                8.609 ns/op
   PASS
  ok      github.com/manulorente/dsa-sample/tests/load    5.250s

In this test, we can see that linear search is faster than binary search when the array is small. This is because binary search has a higher overhead than linear search. However, as the size of the array increases, binary search becomes faster than linear search. This is because binary search eliminates half of the array each time it checks a value, so let’s see the results of the test with an array of 100000 elements:

   manu@msi:~/Projects/dsa-sample$ make test-load 
   goos: linux
   goarch: amd64
   pkg: github.com/manulorente/dsa-sample/tests/load
   cpu: AMD Ryzen 7 5825U with Radeon Graphics         
   BenchmarkLinearSearchSorted-16             24285             50476 ns/op
   BenchmarkLinearSearchUnordered-16          89139             72099 ns/op
   BenchmarkBinarySearchSorted-16          79832916                13.65 ns/op
   PASS
  ok      github.com/manulorente/dsa-sample/tests/load    11.110s

In this test, we can see that binary search is faster than linear search when the array is large and ordered. Although the number of iterations (steps) in binary search is higher than in linear search, the time it takes to complete the search is lower because binary search eliminates half of the array each time it checks a value so the time per operation (ns/op) is lower.

These results can lead into a general rule of thumb: if the array is small, linear search is faster than binary search (or similar at least). If the array is large, binary search is faster than linear search.

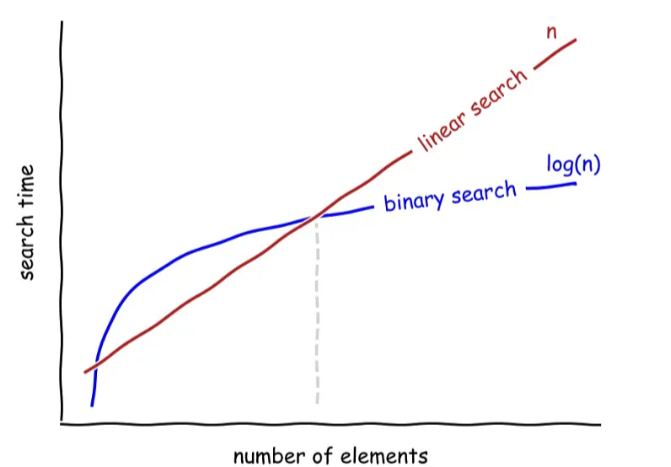
It’s very common to analyze a bunch of graphs that look like this, so let’s take a moment to digest what is going n. The x-axis represetns the number of elements inside the array, as we move from left to right, the number of elements increases. The y-axis represents the time it takes to complete the search, as we move from bottom to top, the time increases.

If we look at the line representing linear search, we can see that as an array has more elements, linear search takes proportionally more time to complete the search. Essentialy, for each additional element in the arrat, linear search takes an additional step to complete the search. This is why the line is a straight line that goes up as the number of elements increases.

On the other hand, if we look at the line representing binary search, we can see that as an array has more elements, binary search takes proportionally less time to complete the search. the algorithm’s steps only increase marginally. We have to double the amount of data in the array to increase the number of steps by one. This is why the line is a curve that goes down as the number of elements increases.

Keeping in ind that ordered arrats aren’t faster in everything, we can say that they are faster in some operations. Insertion and deletion in ordered arrays are slower than in classic arrays, but searching is faster. This is why we need to consider the operations we’ll be performing on the array when we decide whether to use an ordered array or a classic array.

Again we must always analyze the problem we are trying to solve and choose the data structure and algorithm that best suits our needs. Will our app be inserting and deleting values frequently? Will it be searching for values frequently? Will it be doing both? These are the questions we need to ask ourselves before we decide on a data structure and algorithm.

All the code is hosted in this dsa-sample repository. Feel free to clone it and play around with the code, thanks for the read!